有一個現代藝術創作者，他的作品主要是以線條將空間分割成一些幾何圖形區域，再對各幾何圖形區域進行著色。
他特別創造了一系列的作品--直線與 45 度角的對話，這些作品以系統化的方式繪製，皆可以精準地重複以手工複製。
其製作方法如下：先取一張長與寬為整數單位長度的矩形紙，在邊上畫出單位刻度；
再將矩形紙輕描出以單位長度為基準的方格，則畫紙將形成一張方格紙。
接下來以畫紙的左下角當作原點，只要指定兩個座標點連起來，即形成畫紙上的一條直線。

此系列畫作的特色如下：

1. 只有水平直線、垂直直線、以及和矩形紙邊成 45 度角的直線。
2. 直線的兩端一定落在矩形紙邊上。
3. 畫紙上被這些直線所分割出來的三角形一定採用不同的顏色。

請你寫一個程式根據創作者所給定直線的端點，計算出圖形中所分割
出的三角形個數，以決定需要採用幾種顏色。
舉例說明如下：取一張 4×4 單位長度的矩形紙如圖一：


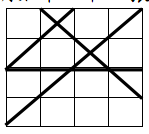
圖一

其水平邊及垂直邊皆為 4 單位長度，畫上去的四條直線的端點分別為

Line 1: (0, 0), (4, 4)
Line 2: (0, 2), (4, 2)
Line 3: (0, 2), (2, 4)
Line 4: (1, 4), (4, 1)

其中分割出的三角形個數為 4。

若取一張 4×6 單位長度的矩形紙如圖二，


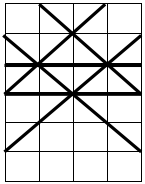
圖二

其水平邊為 4 單位長度，垂直邊為 6 單位長度，畫上去的六條直線的端點分別為

Line 1: (0, 1), (4, 5)
Line 2: (0, 3), (4, 3)
Line 3: (0, 4), (4, 4)
Line 4: (0, 3), (3, 6)
Line 5: (0, 5), (4, 1)
Line 6: (1, 6), (4, 3)

其中分割出的三角形個數為 11。