b066.
5. 六芒星棋遊戲:先還是後比較有利?
內容
在一個稱為『六芒星』的星球上,流行著一種『六芒星棋』的遊戲。這種遊戲是由兩個人來比賽,道具是一個棋盤(如圖一)和13 個鐵圈。遊戲的起始狀態是由兩人互相協調或隨機決定,使用m 個(1 ≤ m ≤ 13)鐵圈在棋盤上圈住 m 個數字。接下來雙方輪流移除棋盤上的鐵圈,每人每次只能移除1 個鐵圈或 2 個相鄰的鐵圈(有直線直接相連的位置視為相鄰),被迫移除最後一個鐵圈的人算輸。
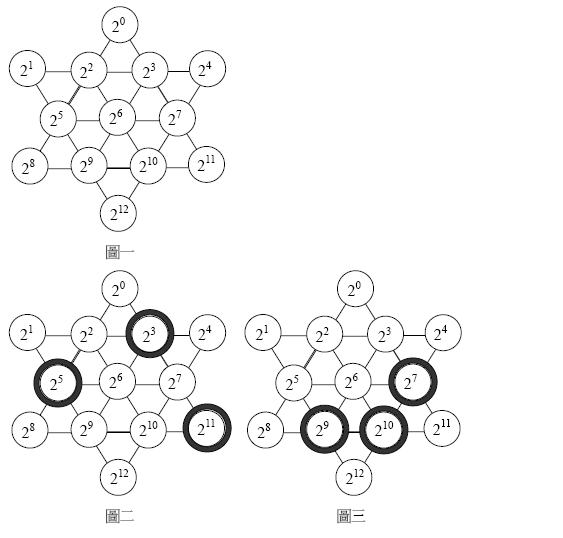
其實如果仔細思考,可以證明不管起始狀態如何,遊戲中先移除鐵圈的人(先手)與其對手(後手)中必定恰有一人,只要他每次都用對自己最有利的方法來移除鐵圈,最後一定百分之百得勝。以起始狀態如圖二為例,因為所有鐵圈均不相鄰,故一次只能移除一個鐵圈,先手不管移除哪一個圈,後手只要再移除一個圈,就可以逼迫先手移除最後一個圈,因此後手有百分之百得勝的把握,我們說成『圖二的起始狀態是後手有利』。若起始狀態如圖三就不同了,如果先手懂得先移除相鄰的兩個鐵圈(如27 與210),就可以迫使後手去移除最後一個圈,因此先手就有百分之百得勝的把握,我們說成『圖三的起始狀態是先手有利』。
每一種起始狀態,我們用一個整數來表示它,這個整數就是在該起始狀態中所有被鐵圈圈住的數字總和。例如圖二的起始狀態可以用23+25+211=2088 表示,圖三則可用27+29+210=1664 來表示。
請你寫一個程式來判斷在不同的起始狀態下,到底是先手還是後手有利。
輸入說明
第一行為一個整數n,1 ≤ n ≤ 10,代表接下來的 n 行中每一行有一個以整數表示的起始狀態。
輸出說明
對每一個輸入的起始狀態,程式必需依順序輸出它們是先手有利(以 1 表示)還是後手有利(以 0 表示)。也就是說,輸出為 n 個 0 或 1 的數字,數字間請用一個空白字元隔開。
範例輸入
#1
3 32 1024 1664 5 6 13 19 2088 2305
範例輸出
#1
0 0 1 1 1 0 0 0
測資資訊:
記憶體限制:
512
MB
公開 測資點#0 (100%): 10.0s , <1K
公開 測資點#0 (100%): 10.0s , <1K
提示 :
標籤:
| 編號 | 身分 | 題目 | 主題 | 人氣 | 發表日期 |
|
沒有發現任何「解題報告」
|
|||||