假设使用者在绘图软体中，使用多边形绘图工具，依序使用滑鼠输入P ₁ 、P ₂ 、…、P _n共n个点的座标，则此绘图工具会自动产生n个相对应的线段（为方便起见，在本题中，我们假设这些线段皆不会与X轴或Y轴平行），分别是P ₁ P ₂ 、P ₂ P ₃ 、…、P _n-1 P _n 、P _n P ₁ 。这n个线段彼此可能相交，也可能没有彼此相交。若我们将这些线段所围起来的所有区域涂上一样的颜色，我们将可以形成一个新的多边形。

例如，在下方的图例中，使用者共依次输入(1,0)、(3,2)、 (0,4)、(3,8)、(2,5)、(1,6)、( 4,7)七个点座标，且这些点座标相对应的线段彼此有相交的现象。若我们将所有线段所围起来的区域涂上一样的颜色后，我们可以得到一个新的11边形，其端点座标分别为(3,8)、(2.5,6.5)、(4,7) 、(2.1111,2.5926)、(3,2)、(1,0)、(2.1111,2.5926)、(0,4)、(1.2857,5.7143)、(1,6)、(1.6667,6.2222)。

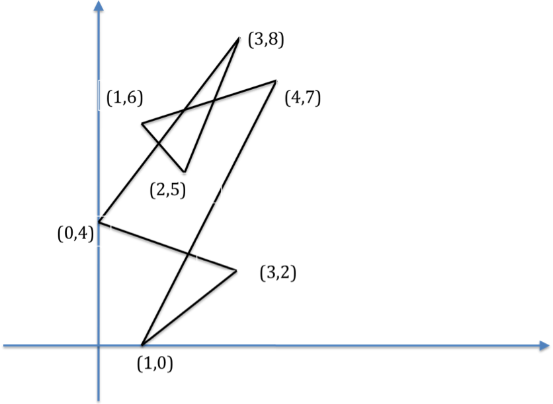
注意，在这个新形成的多边形中，有些端点可能会重复出现。例如，在这个范例中，(2.1111,2.5926)因为刚好是两个线段的交会处，并且是两个子多边形的连接点，因此在新形成的多边形中，共出现了两次。

您的任务是根据依序输入的n个点座标，计算所形成的新的多边形共有几个端点。