內容
一個程式的執行與程序呼叫(procedure invocation)關係，可以描述成一個流程圖形(flow graph)
例如以下程式，將計算Fibonacci 數值
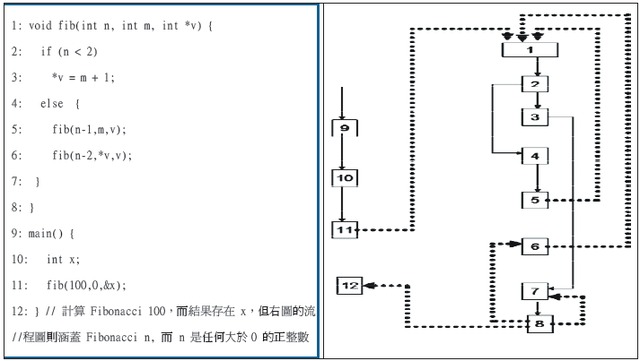
觀察上述程式，每一行指令左邊的數字代表行號（行號為自然數n，若進行函數呼叫時，其返回行號為n+1）
則其流程關係，依照指令的執行先後，可分成程序內部的流程(intra-procedure flow)與跨越程序的流程(inter-procedure flow)。
上述流程圖中，實線表示為程序內部的流程，虛線表示為跨越程序的流程
若遇到程序呼叫(procedure invocation)、與程序結束(procedure return)，則產生跨越程序流程
而程序結束時將回到程序呼叫的下一行。考慮之路徑包含所有實線與虛線的流程。
根據上例，行號9 為程式起點，而行號12 為程式結束，以圖形(graph)的路徑(path) 觀點
從端點9 為起點到終點12，可以有不同路徑。
例如路徑9 10 11 1 2 3 7 8 12 為一種走法，我們稱為合法路徑(valid path)
而9 10 11 1 2 4 5 1 2 3 7 8 12 也是一種走法，但因為不合乎程序呼叫的原則
（呼叫程序後，必須返回原呼叫點的下一行）我們稱為不合法路徑(invalid path)。
針對上述程式範例，根據其流程關係所形成之圖形，給予任一由起點到終點的路徑
（只考慮程序進入點與離開點相匹配，也就是呼叫函數後，返回點必須是呼叫點的下一行。不考慮遞迴的次數）
請你寫一個程式來判斷路徑是否為合法。
輸入說明
測試檔有許多行，除最後一行外，每行包含一個路徑輸入描述，以序列的行號表示。
行號間以一個或以上的空白隔開，一個路徑描述不會超過100 個數字
例如：
9 10 11 1 2 3 7 8 12
9 10 11 1 2 4 5 1 2 3 7 8 12
最後一行只有包含0 一個整數，代表測試檔案的結束。
輸出說明
根據上述範例程式所形成之圖形，依序判斷所給定之路徑是否合法。若合法
輸出：
valid
否則輸出：
invalid
範例輸入
#1
9 10 11 1 2 3 7 8 12 9 10 11 1 2 4 5 1 2 3 7 8 12 9 10 11 12 9 10 11 1 2 4 5 1 2 3 7 8 6 1 2 3 7 8 7 8 12 0
範例輸出
#1
valid invalid invalid valid
測資資訊：
記憶體限制：
512
MB
提示 ：
標籤:
| 編號 | 身分 | 題目 | 主題 | 人氣 | 發表日期 |
|
沒有發現任何「解題報告」
|
|||||