發表新討論
#10986: 解題心得


a5083 (assassin刺客大師)

學校 : 新北市立板橋高級中學
編號 : 28347
來源 : [140.116.138.99]
最後登入時間 ：
2017-06-27 17:13:56
a871. 11. Museum Area -- HP CodeWars2010 | From: [140.123.58.196] | 發表日期 : 2016-06-03 16:32

相信各為遇到這一題最大的問題是怎麼判斷各點的順時針逆時針關係

我查了一下資料後，得到一些小心得

寫在下面給各位參考

首先我們知道三度空間的外積，會因為向量a 向量b順時針或逆時針旋轉的關係而有相反結果

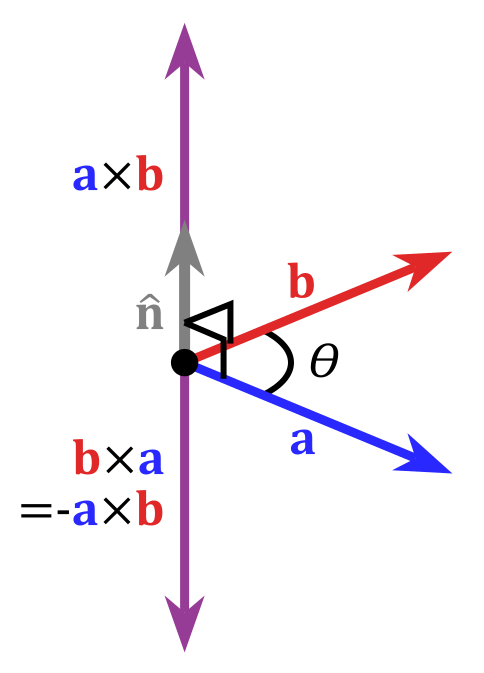
那如果是二為向量外積呢

這裡我引用百度查到的推導

可以自己畫圖並代入數字計算

我們會發現如果二維向量a 外積 b > 0 則 a順時針旋轉到b

反之若二維向量a 外積 b < 0 則 a逆時針旋轉到b

有了這個關係式，就可以將所有點排序成順時針或逆時針旋轉

接下來拆解三角形求面積就很簡單囉

 

 
#15279: Re:解題心得


wish.rirf@gmail.com (C++ 與我)

學校 : 臺北市私立薇閣高級中學
編號 : 82132
來源 : [36.224.41.96]
最後登入時間 ：
2021-08-07 19:29:31
a871. 11. Museum Area -- HP CodeWars2010 | From: [114.136.13.201] | 發表日期 : 2018-09-25 18:05

相信各為遇到這一題最大的問題是怎麼判斷各點的順時針逆時針關係

我查了一下資料後，得到一些小心得

寫在下面給各位參考

首先我們知道三度空間的外積，會因為向量a 向量b順時針或逆時針旋轉的關係而有相反結果

那如果是二為向量外積呢

這裡我引用百度查到的推導

可以自己畫圖並代入數字計算

我們會發現如果二維向量a 外積 b > 0 則 a順時針旋轉到b

反之若二維向量a 外積 b < 0 則 a逆時針旋轉到b

有了這個關係式，就可以將所有點排序成順時針或逆時針旋轉

接下來拆解三角形求面積就很簡單囉

 

鞋帶公式不就可以了嗎

 
ZeroJudge Forum