問題敘述：
  社會學家在研究一個社群時，常會用一個圖形 (graph) 來表示組成該社群人員之間的關係結構。一個標準的表示方式是：社群中每一個成員用圖形的一個頂點 (vertex) 來表示，而社群中的兩個人若有一特定關係則在這兩人相對的頂點間加一個邊 (edge) 來表示這個關係。而有了這樣的圖形表示法，社會學家就可以就這圖形的結構來進行一些研究。
 有一種研究是要在社群中找關鍵人物，有關關鍵人物的認定有各式各樣的方式，其中有一種理論認為一個人若是一個關鍵人物那麼在社群中的很多聯繫都要透過這個人才能完成。因此基於這個觀點，有人提出一個假說：一個人若是一個關鍵人物，那麼他在社群關係圖形中相對的頂點就會有最多條最短路徑( shortest path) 通過。
     現有一個社會學家想要檢測這個理論的正確性，因此他希望你能寫個程式幫他找到社群中的可能關鍵人物。很湊巧的這社會學家找來的社群關係圖形都是樹狀的。我們都知道在樹狀圖 (tree) 中任何兩個頂點間只有唯一一條路徑，因此這路徑當然就是最短路徑。舉例來說，考慮以下樹狀圖：

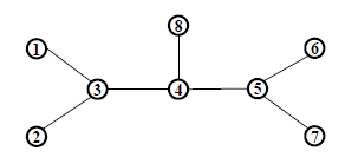
這個圖形共有 8 個頂點，編號從 1 到 8。任何兩個頂點間都有一條路徑，因此這圖形共有 28 條路徑。頂點 1、2、6、7、8 是樹葉節點，因此沒有任何路徑通過。點 3 及頂點 5 分別都有 11 條路徑通過，而頂點 4 則有 15 條路徑通過，因此根這個理論頂點 4 所代表的人物就是關鍵人物，而此點也稱為此圖的關鍵頂點。